測量士補 過去問
令和7年度（2025年）
問26
問題文
図26は、川沿いの平たんな土地における、円曲線始点A、円曲線終点Bからなる円曲線の道路の建設計画を模式的に示したものである。
交点IPの位置に川が流れており、杭を設置できないため、円曲線始点Aと交点IPを結ぶ接線上に補助点C、円曲線終点Bと交点IPを結ぶ接線上に補助点Dをそれぞれ設置し観測を行ったところ、α＝95°、β＝145°であった。
曲線半径R＝350mとするとき、円曲線始点Aから円曲線終点Bまでの路線長は幾らか。最も近いものを次の選択肢から選べ。
なお、円周率＝3.14とし、関数の値が必要な場合は、関数表を使用すること。
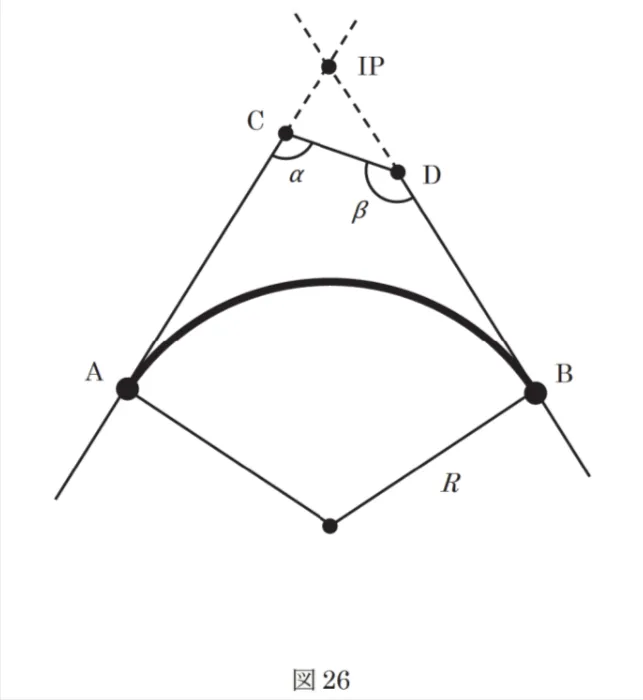
交点IPの位置に川が流れており、杭を設置できないため、円曲線始点Aと交点IPを結ぶ接線上に補助点C、円曲線終点Bと交点IPを結ぶ接線上に補助点Dをそれぞれ設置し観測を行ったところ、α＝95°、β＝145°であった。
曲線半径R＝350mとするとき、円曲線始点Aから円曲線終点Bまでの路線長は幾らか。最も近いものを次の選択肢から選べ。
なお、円周率＝3.14とし、関数の値が必要な場合は、関数表を使用すること。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
測量士補試験 令和7年度（2025年） 問26 （訂正依頼・報告はこちら）
図26は、川沿いの平たんな土地における、円曲線始点A、円曲線終点Bからなる円曲線の道路の建設計画を模式的に示したものである。
交点IPの位置に川が流れており、杭を設置できないため、円曲線始点Aと交点IPを結ぶ接線上に補助点C、円曲線終点Bと交点IPを結ぶ接線上に補助点Dをそれぞれ設置し観測を行ったところ、α＝95°、β＝145°であった。
曲線半径R＝350mとするとき、円曲線始点Aから円曲線終点Bまでの路線長は幾らか。最も近いものを次の選択肢から選べ。
なお、円周率＝3.14とし、関数の値が必要な場合は、関数表を使用すること。
交点IPの位置に川が流れており、杭を設置できないため、円曲線始点Aと交点IPを結ぶ接線上に補助点C、円曲線終点Bと交点IPを結ぶ接線上に補助点Dをそれぞれ設置し観測を行ったところ、α＝95°、β＝145°であった。
曲線半径R＝350mとするとき、円曲線始点Aから円曲線終点Bまでの路線長は幾らか。最も近いものを次の選択肢から選べ。
なお、円周率＝3.14とし、関数の値が必要な場合は、関数表を使用すること。
- 672m
- 702m
- 733m
- 763m
- 794m
正解！素晴らしいです
残念...
この過去問の解説 （2件）
01
順番に計算していきましょう。
１．IP（交点）の内角を求めます
交点 IP は、補助点 C–A と D–B の接線線分で交わる点です。
その交点での「角度 θ」は、
θ=360°−(α+β)=360°−(95°+145°)=360°−240°=120°
2. 円曲線の中心角 Δ を求めます
Δ=180°−θ=180°−120°=60°
3. 曲線の弧長を求めます
L=π×R×Δ/180°=π×350×60/180=π×350×1/3=366.52m
4. A→B 全体の路線長を考えます
問題文で「始点 A から終点 B まで」は、この曲線を両側から測る構造になってることから、この弧長 × 2で路線長を求めます。
LAB=2×366.52=733.04m
よって、答えは733mになります。
参考になった数1
この解説の修正を提案する
02
以下、解答です。
不正答です。
不正答です。
正答です。
不正答です。
不正答です。
・路線長の求め方
円曲線の路線長は曲線の中点から始点までの弧長の2倍で計算できます。
途中に補助点C、Dがあり、観測角度 α と β を使います。
①交点IPの内角θ
θ=360°−(α+β)=360°−(95°+145°)=120°
②円曲線の中心角Δは
Δ=180°−θ=180°−120°=60°
③路線長L
弧長なので、曲線半径と中心角から求めます。
L=π×R×Δ/180°=π×350×60/180=π×350×1/3≈366.52m
④頭頂点Aから終点Bまでの路線長は、2倍の弧長
LAB=2×366.52=733.04m
参考になった数0
この解説の修正を提案する
前の問題（問25）へ
令和7年度（2025年） 問題一覧
次の問題（問27）へ